Evolving Cellular Automata

This post is about evolving Cellular Automata to perform computation. The example I use is from the book Complexity - A Guided Tour

The most famous cellular automata is Conway’s Game of Life, a 2D automaton with simple rules to determine whether each cell lives or dies on each iteration based on the adjacent cells.

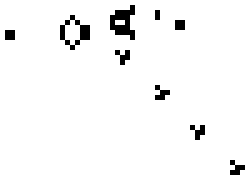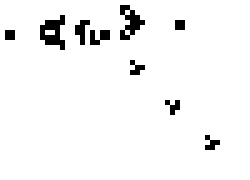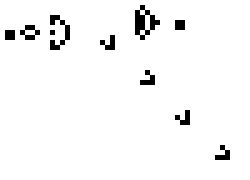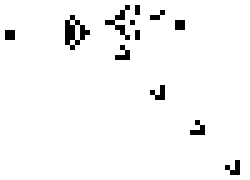
Above is the well known Glider Gun that is at the heart of many complex Life configurations, including a Universal Computer. A perfect example of complex results arising from simple rules.

The automata we are looking at today are much simpler and one dimensional.

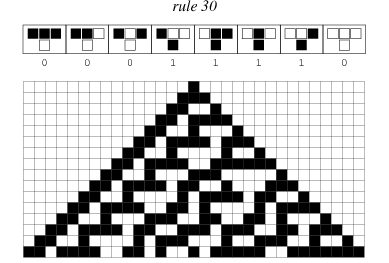
Above is ‘rule 30’, so called because of its Wolfram Code (see here on the Mathworld site for more information). It is a binary (has two states), nearest-neighbour (each cell can “see” its 2 neighbours), one-dimensional automaton. As you can see it can be in 8 ($2^{3}$) different states and the binary below it is equal to 30. The bottom half of the picture is a 'space-time’ diagram, the top row is the initial configuration and each row beneath represents the next step after each cell lives or dies according to its rule.

The Majority Problem

The 1D automata I am interested in are binary also, but each cell’s neighbourhood includes its 3 adjacent neighbours on both sides (ie $2^{7} = 128$ different states as it can see itself and 6 neighbours). The world wraps like a torus so the 0th cell is adjacent to the 100th in our 101 cell world. The problem that we want to solve is the Majority Problem, ie if the initial configuration is mostly alive/dead after some number of steps all should be alive/dead, if so then the rule has successfully performed the task.

Go here and watch it evolve if you have not already.

How well we do the task?

The best human created rule is by Gács, Kurdyumov, and Levin

If a cell is 0, its next state is formed as the majority among the values of itself, its immediate neighbour to the left, and its neighbor three spaces to the left. If, on the other hand, a cell is 1, its next state is formed symmetrically, as the majority among the values of itself, its immediate neighbor to the right, and its neighbor three spaces to the right.

As you can hopefully see it is quite successful. In order to determine what the majority was information needs to be passed across the cells and can only travel at a maximum speed, rather like light in our universe. The interactions are best described in terms of particles being created and destroyed, again quite like our universe under quantum theory.

(By the way all these images are actual simulations working in your browser now… which is perhaps why it wont work in FireFox…)

Can a genetic algorithm do any better?

There are $2^{128}$ different genomes (remember there are 128 different possible states and you can transition to either of 2 states from each one). This is a huge search space but genetic algorithms can indeed do very well at the task and uncover some great tricks along the way.

Random

For the following “Fitness X” means it correctly classifies X% of the initial starting conditions when you first pick a probability p at random then make p% of the initial cells live. Random starting positions cluster around the 50/50 mark and are harder on average than ones picked this way.

Fitness 10

Fitness 30

Fitness 50

It sticks here for a while as getting 50% right is easy if you always go alive or always dead.

Fitness 60

Fitness 70

Fitness 80

Fitness 90

Fitness 97

It is proven that it is not possible to be 100% (see the Wikipedia article referenced above) but it’s pretty good isn’t it!

I was going to talk about the code but I think this is long enough for one post, I hope you found it interesting.

Please go to this page to help evolve a solution.

Code is on github if you want to take a peek now.

Go to the followup article to see the code