Genetic Programming In Clojure With Zippers
August 23, 2013
This post is another update to my Lisp In Summer Projects project. I blogged before (1 2) about warm-up exercises but I have not yet explained the goal, I intend writing an Artificial Life simulation where the organisms themselves are Lisp programs that runs (via clojurescript) inside peoples browsers.
You may also want to check out a video of a talk I gave (in part) about this stuff for the london clojurians, slides here
After doing Genetic Algorithms, both in Coffeescript and Clojurescript the next step was to look at Genetic Programming. GP is the same as GA except that the genome is the AST of a programming language (Lisp makes it easier as S-Expressions are directly manipulable).
Take a look a the Wikipedia Article before we continue with how I did it in Clojure using zippers.
As I said in the other post about GA, the basic idea is to:
- find a way to encode a particular solution to the problem as a genome
- start with an initial population of random genomes
- work out their ‘fitness’ (ie how well they perform some task)
- choose the next generation by selecting and ‘breeding’ them (with some mutation for novelty)
- repeat until a good solution appears
In the GP world the first step changes, the initial genomes are valid programs rather than fixed length byte sequences. The ‘breed’ function is more complicated too, where before we could get away with choosing a random ‘split point’ and taking the left part of one and the right part of its mate and vice versa we have to be careful about where we slit and how we join the S-Expressions, also the length is not bounded anymore.
Enter The Zipper
In Clojure zippers are found in clojure.zip and I’ll quote the description given there:
A zipper is a data structure representing a location in a hierarchical data structure, and the path it took to get there. It provides down/up/left/right navigation, and localized functional ‘editing’, insertion and removal of nodes. With zippers you can write code that looks like an imperative, destructive walk through a tree, call root when you are done and get a new tree reflecting all the changes, when in fact nothing at all is mutated - it’s all thread safe and shareable. The next function does a depth-first walk, making for easy to understand loops.
See also Wikipedia and FUNCTIONAL PEARL - The Zipper (Huet 97)
In summary the operations defined are:
(seq-zip root)
;; Returns a zipper for nested sequences, given a root sequence
(vector-zip root)
;; Returns a zipper for nested vectors, given a root vector
(xml-zip root)
;; Returns a zipper for xml elements (as from xml/parse),
;; given a root element
(root loc)
;; zips all the way up and returns the root node, reflecting any changes.
(node loc)
;; Returns the node at loc
(next loc)
;; Moves to the next loc in the hierarchy, depth-first.
;; When reaching the end, returns a distinguished loc detectable via end?
;; If already at the end, stays there.
(replace loc node)
;; Replaces the node at this loc, without moving
(edit loc f & args)
;; Replaces the node at this loc with the value of (f node args)
;; You can probably guess what these do
(prev loc)
(down loc)
(up loc)
(left loc)
(remove loc)
(leftmost loc)
(lefts loc)
(insert-left loc item)
(insert-child loc item)
I have mentioned the seq-zip, xml-zip and vector-zip functions there but the more generic way to create them is the zipper function.
(zipper branch? children make-node root)
;; Creates a new zipper structure.
;; branch? is a fn that, given a node, returns true if can have
;; children, even if it currently doesn't.
;; children is a fn that, given a branch node, returns a seq of its
;; children.
;; make-node is a fn that, given an existing node and a seq of
;; children, returns a new branch node with the supplied children.
;; root is the root node.
A few examples so we get a sense how zippers work, eg is an s-expression and we call seq-zip on it to get a zipper.
> eg
(* (+ 1 2) (- (* 3 4) (+ 5 (+ 6 7))))
> (def z (zip/seq-zip eg))
We can get a list of ‘locations’ by calling next until end? is true.
> (def locs (take-while (complement zip/end?) (iterate zip/next z)))
> (doseq [loc locs]
(println (zip/node loc)))
(* (+ 1 2) (- (* 3 4) (+ 5 (+ 6 7))))
*
(+ 1 2)
+
1
2
(- (* 3 4) (+ 5 (+ 6 7)))
-
(* 3 4)
*
3
4
(+ 5 (+ 6 7))
+
5
(+ 6 7)
+
6
7
As you can see the locations are sometimes subtrees, sometimes individual values and we get them in depth-first order.
Here we call next 4 times on our zipper z, and send the inc function to that location via edit, then ask for the result by calling root
> eg
(* (+ 1 2) (- (* 3 4) (+ 5 (+ 6 7))))
> (zip/root (zip/edit (nth (iterate zip/next z) 4)
inc))
(* (+ 2 2) (- (* 3 4) (+ 5 (+ 6 7))))
Here we call next twice and replace that location (ie the (+ 1 2) subtree) with :swapped
> eg
(* (+ 1 2) (- (* 3 4) (+ 5 (+ 6 7))))
> (-> z
zip/next
zip/next
(zip/replace :swapped)
(zip/root))
(* :swapped (- \(* 3 4) (+ 5 (+ 6 7))))
Breeding S-Expressions
The below picture (from the A Field Guide To Genetic Programming) gives the idea: choose a location on each tree, and replace with a location from the other tree.
The (/ x 2) is inserted where the (+ x 1) was in this case. Also you don’t need to ‘throw away’ half of each genome, we could have in this case assembled (* (+ y 1) (+ x y)) from the other parts of the s-expressions.
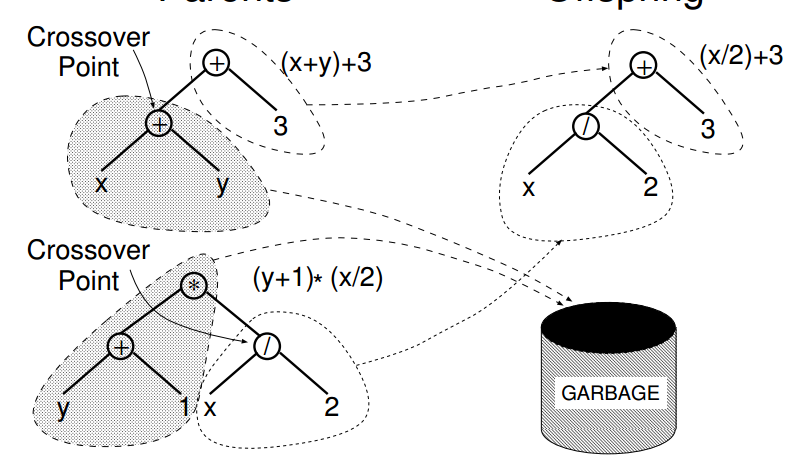
Take care however as not all the locations can be easilly swapped out, the first element in an s-expression is supposed to be a function remember.
My first attempt is below, the The idx-to-loc function works by only looking at the branches and going up if it is a function (to get the whole subtree)
(def fns #{'+ '* '-})
(defn idx-to-loc [tree idx]
(let [z (zip/seq-zip tree)
loc (nth (filter (complement zip/branch?) (iterate zip/next z)) idx)]
(if (fns (zip/node loc))
(zip/up loc)
loc)))
(defn subtree [t idx]
(zip/node (idx-to-loc t idx)))
(defn breed [L R]
(let [sizeL (count (flatten L))
sizeR (count (flatten R))
zipL (zip/seq-zip L)
zipR (zip/seq-zip R)
posL (rand-int sL)
posR (rand-int sR)
subL (subtree L posL)
subR (subtree R posR)
]
[(zip/root (zip/replace (idx-to-loc L posL)
subR))
(zip/root (zip/replace (idx-to-loc R posR)
subL))]))
In words we: ‘get the size of each s-expression, make zippers of them, choose a random location of each, take the subtree at that point, replace in the left s-expression the subtree we took of the right and vice versa’
While not too awful, this can be improved upon and I arrived at:
(def fns #{'+ '* '-})
(defn locs [G]
(let [zipper (zip/seq-zip G)
all-locs (take-while (complement zip/end?) (iterate zip/next zipper))]
(filter #(not (fns (zip/node %))) all-locs)))
(defn replace-loc [l r]
(zip/root (zip/replace l (zip/node r))))
(defn breed [L R]
(let [l (rand-nth (locs L))
r (rand-nth (locs R))]
[(replace-loc l r) (replace-loc r l)]))
Here the breed function is a bit clearer, in words ‘take a random
location in both nodes, replace in the left location the node value
of the right location and vice versa. The locs function is also
clearer, taking every location that is not a function.
Testing the new locs function to see if it works:
> eg
(* (+ 1 2) (- (* 3 4) (+ 5 (+ 6 7))))
> (doseq [loc (locs g2)]
(println (zip/node loc)))
(* (+ 1 2) (- (* 3 4) (+ 5 (+ 6 7))))
(+ 1 2)
1
2
(- (* 3 4) (+ 5 (+ 6 7)))
(* 3 4)
3
4
(+ 5 (+ 6 7))
5
(+ 6 7)
6
7
Breeding s-expressions
> g1
(+ x (* x 1))
> g2
(+ 2 3 (* 4 x) x)
> (breed g1 g2)
[(+ x (* 4 1))
(+ 2 3 (* x x) x)]
[x
(+ 2 3 (* 4 x) (+ x (* x 1)))]
[(+ x (* x 1))
(+ 2 3 (* 4 x) x)]
[(+ x (* (+ 2 3 (* 4 x) x) 1))
x]
[(+ 2 3 (* 4 x) x)
(+ x (* x 1))]
[(+ x (* x 2))
(+ 1 3 (* 4 x) x)]
[(+ x 2)
(+ (* x 1) 3 (* 4 x) x)]
Hello World
The Hello World of GP is finding functions that approximate polynomials. I will be looking for $x^2 + x + 1$ with the functions + - * and random numbers between -5 and 5.
Creating the initial population
(defn random-fn []
(rand-nth fns))
(defn random-terminal []
(if (< (rand) 0.5)
'x
(- (rand 10) 5)))
(defn random-code
([] (random-code 2))
([depth]
(if (zero? (rand-int depth))
(cons (random-fn)
(repeatedly 2
#(random-code (inc depth))))
(random-terminal))))
Working out fitness:
(defn to-fn [g]
(eval (list 'fn '[x] g)))
(defn error
[individual]
(let [value-function (to-fn individual)]
(reduce + (map (fn [[x y]]
(Math/abs
(- (value-function x) y)))
target-data))))
Selection, here we use ‘tournament selection’ which abstractly means you take n different genomes, run the simulations and see who does best but as a speedup we calculate all fitnesses at the beginning, choose n integers, find the smallest (call it s) and take the genome in the s’th position.
(defn sort-by-error
[population]
(vec (map second
(sort (fn [[err1 ind1] [err2 ind2]] (< err1 err2))
(map #(vector (error %) %) population)))))
(defn select
[population tournament-size]
(let [size (count population)]
(nth population
(apply min (repeatedly tournament-size #(rand-int size))))))
The Main Loop:
(defn evolve
[popsize]
(println "Starting evolution...")
(loop [generation 0
population (sort-by-error (repeatedly popsize #(random-code)))]
(let [best (first population)
best-error (error best)]
(println "Generation:" generation)
(println "Best error:" best-error)
(println "Best program:" best)
(if (< best-error 0.1)
(println "Success:" best)
(recur
(inc generation)
(sort-by-error
(concat
(repeatedly (* 1/2 popsize) #(mutate (select population 7)))
(repeatedly (* 1/4 popsize) #(breed (select population 7)
(select population 7)))
(repeatedly (* 1/4 popsize) #(select population 7)))))))))
Results
Generation: 86
Best error: 0.0012624873111660717
Best program: (+ (* x x)
(+ (+ (+ x -0.00569678366123938)
-0.00569678366123938)
1.0114536857658676))
Average program size: 8.574
Sometimes we have ‘junk dna’
(- (+ (+ 1.030006977532941 (+ (* x x) x)) -0.03253646108577968)
(* (- x x) (+ (+ (* x -3.1929113275788) x) x)))
(see the (- x x) in there?)
In The Browser?
I got it working in clojurescript but it was too slow to embed in this page to have it work while you read the post, maybe I’ll have to not use zippers for my project.
Attribution
Lee Spector of Hampshire College had also done GA with zippers and I came across a project of his when looking for prior art. While I did the actual breed function differently lots of the other bits (and the example) are taken directly from his project.
He has actually added more since I first saw it you should check it out